 |
Our attitude is that in best practice classrooms all students can learn to work like a mathematician. On this page we detail the meaning of Working Mathematically and include illustrations from classrooms and learners of all ages.
 Working Mathematically Process
From Teachers & Schools
Notes from an Inspector's Notebook
Working Mathematically Anthem
|
Eric The Sheep, Year 3 Kingsley Park Primary School, Victoria
|
The process of Working Mathematically - learning to work like a mathematician - is the scaffold for all our services and resources. In its early days the Task Centre Project asked professional mathematicians to detail what they did. We compiled their responses to create our statement of the:
Working Mathematically Process
First give me an interesting problem.
When mathematicians become interested in a problem they:
- Play with the problem to collect & organise data about it.
- Discuss & record notes and diagrams.
- Seek & see patterns or connections in the organised data.
- Make & test hypotheses based on the patterns or connections.
- Look in their strategy toolbox for problem solving strategies which could help.
- Look in their skill toolbox for mathematical skills which could help.
- Check their answer and think about what else they can learn from it.
- Publish their results.
Questions which help mathematicians learn more are:
- Can I check this another way?
- What happens if ...?
- How many solutions are there?
- How will I know when I have found them all?
When mathematicians have a problem they:
- Read & understand the problem.
- Plan a strategy to start the problem.
- Carry out their plan.
- Check the result.
A mathematician's strategy toolbox includes:
- Do I know a similar problem?
- Guess, check and improve
- Try a simpler problem
- Write an equation
- Make a list or table
- Work backwards
- Act it out
- Draw a picture or graph
- Make a model
- Look for a pattern
- Try all possibilities
- Seek an exception
- Break the problem into smaller parts
- ...
If one way doesn't work I just start again another way.
|
Working Mathematically (PDF)
Arbeta Matematiskt (PDF)
If you think this flow chart might support you in creating a Working Mathematically curriculum, open
Creating Working Mathematically Curriculum
for more information.
Working Mathematically Curriculum Scaffold
might also be a useful document and
you can catch the vision of Working Mathematically at:
Click the logo to find videos presenting images of
working like a mathematician.
|
From Teachers & Schools
In Praise of Working Mathematically
After participating in our workshops at the 2009 conference of the Association of Teachers of Mathematics, UK, Steve Watson, Lincolnshire, began exploring the concept of learning to work like a mathematician with his students in a rural secondary school. Six months later, excited by his classroom successes, he sent an email with the subject line In Praise of Working Mathematically which began:
I have become very interested in the Task Centre, since I came to see you talk at the ATM conference in April. I have used your idea of Working Mathematically, adapting it slightly to a 'Problem-play-results-communicate' cycle. I am becoming increasingly confident that teaching students to learn to think mathematically is intrinsically motivating and helps students make excellent progress. I am teaching less 'mathematical methods'.
A couple of weeks later he wrote:
I was at AQA (one of the main examining boards) they were pushing the idea of Working Mathematically quite heavily. They were also suggesting that unless students were taught to problem solve they wouldn't be able to perform well on the new GCSE that is coming out in 2010. During one of the sessions I started to think about how our key processes and functional maths in England connect to the idea of Working Mathematically. The attached diagram shows this mapping, quite simply.
Consider Steve's Diagram. (This is a PDF file - use the View/Rotate/Clockwise menu once you have opened it.) The diagram will be most relevant to teachers from England and Wales, but its existence helps to explain why Working Mathematically (see above) blends with and strengthens the curriculum requirements of any system.
In other words, across the world, all students can be learning to work like a mathematician in best practice classrooms. There is no reason for mathematics to be taught the way it always has been.
Mathematician's Tool Shed
Harry Kanasa, John Paul College, Queensland, has taken the strategy toolbox section above and turned it into a Strategy Tool Shed. The visual nature of the presentation will add meaning for many students, and the addition of the multiple intelligences checklist will appeal to many teachers.
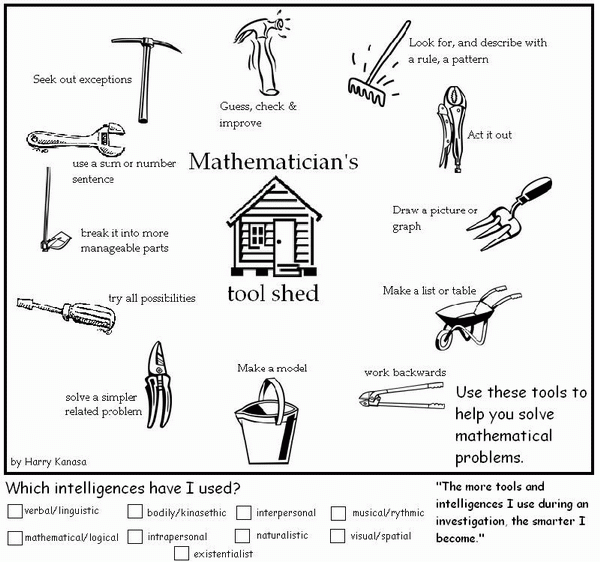Harry is very happy for others to make use of this creation, so if you would like to save it:
- Click the drawing to call up a higher resolution version, then
- Right click (Windows) or click and hold (Mac) and choose Save Picture As...
Benalla College Charter
Benalla College, Victoria, Australia is one school that has used our professional services to help the staff shift towards a Working Mathematically curriculum. This is the charter they developed:
Maths Charter
WORKING MATHEMATICALLY
STATEMENT
WE WANT TO SHIFT OUR MATHS CURRICULUM TO ONE THAT REFLECTS:
- Active engagement of students through 'hands on' activities and demonstrations using the model of 'working mathematically'.
- Mathematics as a 'visual', motivating, challenging learning experience!
- Building on the knowledge students bring to the classroom and is relevant to the students.
- Stimulates students' curiosity through the use of diverse materials and tasks.
- Responds and caters to the individual needs of each student from concrete to abstract thinkers.
- Student ownership in the Maths classes achieved by providing a structured, relaxed, supportive and open atmosphere where students are encouraged to be active problem solvers and are able to justify and explain, without fear, where they are at.
- Students experiencing 'success' and 'feeling good' about doing Maths by 'modeling' their work to their peers.
- Evidence of achievement in response to a task as measured against previously published outcome expectations.
|
Notes from an Inspector's Notebook
John Hibbs is a retired HMI (Her Majesty's Inspector) and lifelong learner and teacher through hands-on problem solving. He is a great supporter of our site and occasionally shares items from his extensive diaries of mathematical adventures journeyed throughout his career. They provide an insight into the way mathematician's think.
|
The image is of Sophie Germain, whose work on Fermat's Last Theorem in 1738 was to remain the most important contribution to the problem for over 100 years until 1840. Click on the image to visit a web site with a complete biography. It is also where we sourced this picture. |
Working Mathematically Anthem
On December 5th, 2002, Doug Williams gave a keynote address to the Annual Conference of the Mathematical Association of Victoria entitled Learning to Work Like a Mathematician. He closed the address with a song. At the request of many present this song has been made available below.
Right Click on the tune and choose Save Link As... to download a Midi file. The text of the address is available in the Web Papers.
(Tune: Advance Australia Fair)
Maths teachers all let us rejoice
Our subject is not trite!
It's far more than the daily toil
Of "Is this wrong or right?"
The theme we weave each time we teach
Must challenge students to
Engage with problems in the way
That math'maticians do!
In joyful classrooms let us work
Like math'maticians do!
|
Alternative arrangements of the tune:
|
|
|
